Package org.apache.datasketches.hll
The DataSketches™ HLL sketch family package
HllSketch and Union
are the public facing classes of this high performance implementation of Phillipe Flajolet's
HyperLogLog algorithm[1] but with significantly improved error behavior and important features that can be
essential for large production systems that must handle massive data.
Key Features of the DataSketches™ HLL Sketch and its companion Union
Advanced Estimation Algorithms for Optimum Accuracy
Zero error at low cardinalities
The HLL sketch leverages highly compact arrays and hash tables to keep exact counts until the transition to dense mode is required for space reasons. The result is perfect accuracy for very low cardinalities.Accuracy for very small streams can be important because Big Data is often fragmented into millions of smaller streams (or segments) that inevitably are power-law distributed in size. If you are sketching all these fragments, as a general rule, more than 80% of your sketches will be very small, 20% will be much larger, and only a few very large in cardinality.
HIP / Martingale Estimator
When obtaining a cardinality estimate, the sketch automatically determines if it was the result of the capture of a single stream, or if was the result of certain qualifying union operations. If this is the case the sketch will take advantage of Edith Cohen's Historical Inverse Probability (HIP) estimation algorithm[2], which was also independently developed by Daniel Ting as the Martingale estimation algorithm[3]. This will result in a 20% improvement in accuracy over the standard Flajolet estimator. If it is not a single stream or if the specific union operation did not qualify, the estimator will default to the Composite Estimator.Composite Estimator
This advanced estimator is a blend of several algorithms including new algorithms developed by Kevin Lang for his Compressed Probabilistic Counting (CPC) sketch[4]. These algorithms provide near optimal estimation accuracy for cases that don't qualify for HIP / Martingale estimation.As a result of all of this work on accuracy, one will get a very smooth curve of the underlying accuracy of the sketch once the statistical randomness is removed through multiple trials. This can be observed in the following graph.
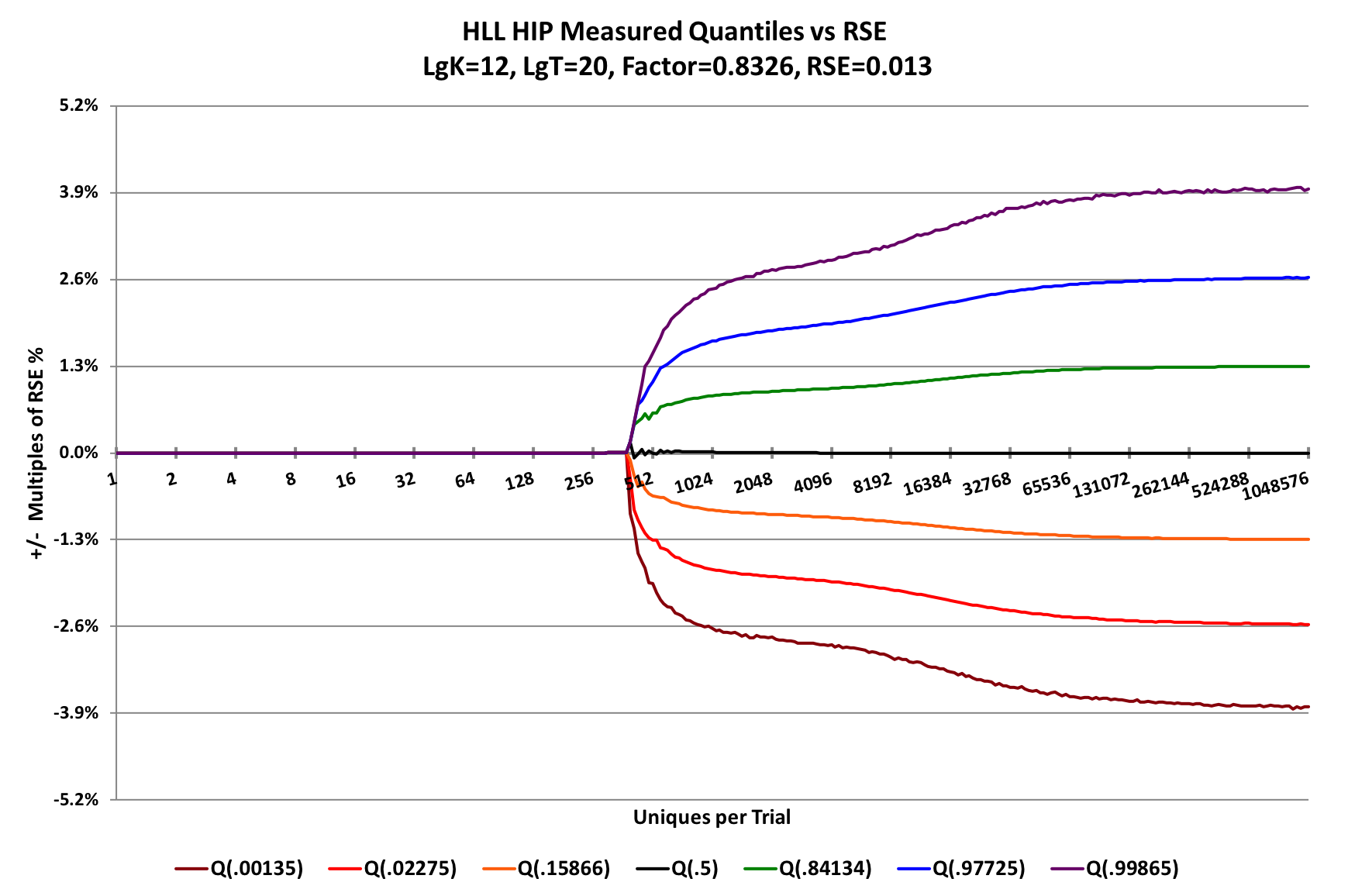 [6]
[6]
The above graph has 7 curves. At y = 0, is the median line that hugs the x-axis so closely that it can't be seen. The two curves, just above and just below the x-axis, correspond to +/- 1 standard deviation (SD) of error. The distance between either one of this pair and the x-axis is also known as the Relative Standard Error (RSE). This type of graph for illustrating sketch error we call a "pitchfork plot".
The next two curves above and below correspond to +/- 2 SD, and the top-most and bottom-most curves correspond to +/- 3 SD. The chart grid lines are set at +/- multiples of Relative Standard Error (RSE) that correspond to +/- 1,2,3 SD. Below the cardinality of about 512 there is no error at all. This is the point where this particular sketch transitions from sparse to dense (or estimation) mode.
Three HLL Types
This HLL implementation offers three different types of HLL sketch, each with different trade-offs with accuracy, space and performance. These types are selected with theTgtHllType parameter.
In terms of accuracy, all three types, for the same lgConfigK, have the same error distribution as a function of cardinality.
The configuration parameter lgConfigK is the log-base-2 of K, where K is the number of buckets or slots for the sketch. lgConfigK impacts both accuracy and the size of the sketch in memory and when stored.
HLL 8
This uses an 8-bit byte per HLL bucket. It is generally the fastest in terms of update time but has the largest storage footprint of about K bytes.HLL 6
This uses a 6-bit field per HLL bucket. It is the generally the next fastest in terms of update time with a storage footprint of about 3/4 * K bytes.HLL 4
This uses a 4-bit field per HLL bucket and for large counts may require the use of a small internal auxiliary array for storing statistical exceptions, which are rare. For the values of lgConfigK > 13 (K = 8192), this additional array adds about 3% to the overall storage. It is generally the slowest in terms of update time, but has the smallest storage footprint of about K/2 * 1.03 bytes.Off-Heap Operation
This HLL sketch also offers the capability of operating off-heap. Given a WritableMemory[5] object created by the user, the sketch will perform all of its updates and internal phase transitions in that object, which can actually reside either on-heap or off-heap based on how it was configured. In large systems that must update and union many millions of sketches, having the sketch operate off-heap avoids the serialization and deserialization costs of moving sketches from heap to off-heap and back, and reduces the need for garbage collection.Merging sketches with different configured lgConfigK
This enables a user to union a HLL sketch that was configured with, say, lgConfigK = 12 with another loaded HLL sketch that was configured with, say, lgConfigK = 14.Why is this important? Suppose you have been building a history of sketches of your customer's data that go back a full year (or 5 or 10!) that were all configured with lgConfigK = 12. Because sketches are so much smaller than the raw data it is possible that the raw data was discarded keeping only the sketches. Even if you have the raw data, it might be very expensive and time consuming to reload and rebuild all your sketches with a larger more accurate size, say, lgConfigK = 14. This capability enables you to merge last year's data with this year's data built with larger sketches and still have meaningful results.
In other words, you can change your mind about what size sketch you need for your application at any time and will not lose access to the data contained in your older historical sketches.
This capability does come with a caveat: The resulting accuracy of the merged sketch will be the accuracy of the smaller of the two sketches. Without this capability, you would either be stuck with the configuration you first chose forever, or you would have to rebuild all your sketches from scratch, or worse, not be able to recover your historical data.
Multi-language, multi-platform.
The binary structures for our sketch serializations are language and platform independent. This means it is possible to generate an HLL sketch on a C++ Windows platform and it can be used on a Java or Python Unix platform.[1] Philippe Flajolet, et al, HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm. DMTCS proc. AH, 2007, 127-146.
[2] Edith Cohen, All-Distances Sketches, Revisited: HIP Estimators for Massive Graphs Analysis. PODS'14, June 22-27, Snowbird, UT, USA.
[3] Daniel Ting, Streamed Approximate Counting of Distinct Elements, Beating Optimal Batch Methods. KDD'14 August 24, 2014 New York, New York USA.
[4] Kevin Lang, Back to the Future: an Even More Nearly Optimal Cardinality Estimation Algorithm. arXiv 1708.06839, August 22, 2017, Yahoo Research.
[5] Memory Component, DataSketches Memory Component
[6] MacBook Pro 2.3 GHz 8-Core Intel Core i9
- Author:
- Lee Rhodes, Kevin Lang
- See Also:
CpcSketch
-
Class Summary Class Description HllSketch The HllSketch is actually a collection of compact implementations of Phillipe Flajolet’s HyperLogLog (HLL) sketch but with significantly improved error behavior and excellent speed performance.Union This performs union operations for all HllSketches. -
Enum Summary Enum Description TgtHllType Specifies the target type of HLL sketch to be created.